Objetivos de aprendizaje
- Determinar cuándo y por qué la distribución de una muestra adquiere una forma acampanada.
- Comprender que la distribución muestral de la media calculada a partir de muestras aleatorias grandes tiende a mostrar un comportamiento regular.
- Comprender cómo el Teorema del Límite Central describe la forma, el centro y la dispersión de la distribución muestral de un estadístico.
Desarrollo
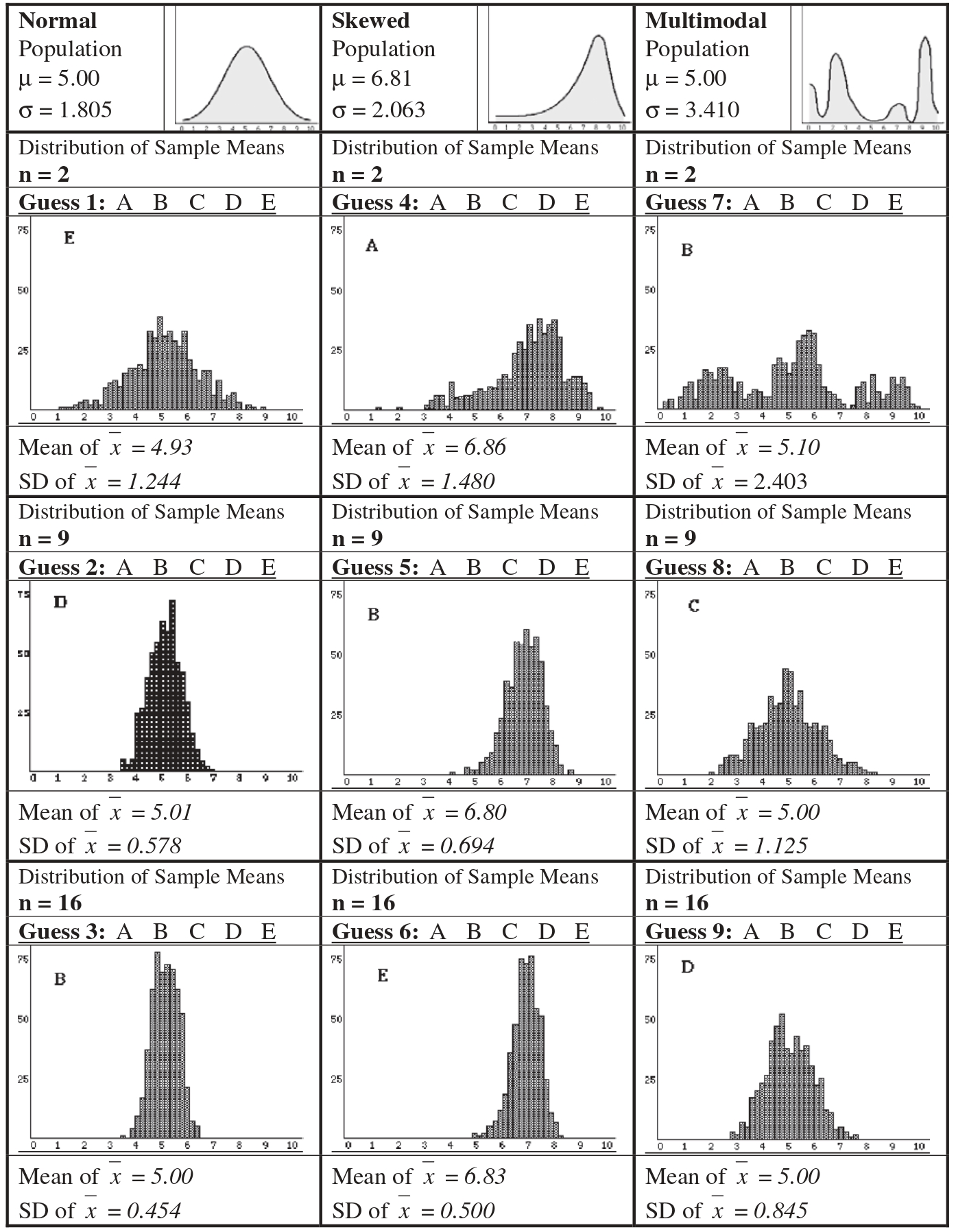
Tu docente te proporcionará dos hojas las cuales utilizarás en esta actividad, una llamada Hoja 1 para el estudiante y otra llamada Hoja 2 para el estudiante. En la Hoja 1 podrás encontrar una tabla en donde cada columna representa el histograma de la media muestral de una población específica considerando diferentes tamaños de muestra pero repitiendo el muestreo 500 veces. En la Hoja 2, se tiene en el primer renglón una descripción de las tres poblaciones diferentes. Si no tienes hojas, puedes localizar las hojas haciendo clic aquí . Tu trabajo es el siguiente:
- En la primera columna de la Hoja 2, vas a subrayar o marcar la distribución muestral de la media que consideras corresponde al tamaño de muestra utilizado, \(n\), y la media y desviación estándar de \(\bar{x}\) con las distribuciones mostradas de la columna 1 de la Hoja 1. Puedes seleccionar A, B, C o D. Hint: para poder responder, presta mucha atención en el tamaño de la muestra que se toma para calcular la medias, así como también la localización y variabilidad de la distribución para poderlas identificar.
- Repite el paso anterior con las columnas 2 y 3 de la Hoja 2, utilizando las respectivas columnas de la Hoja 1.
- Recorta los cuadritos de las gráficas de la Hoja 1.
- Ingresa al siguiente applet, y verifica las respuestas que subrayaste o circulaste en la Hoja 2 seleccionando en el applet el tipo y tamaño de la muestra.
- Una vez que identifiques qué gráfica debe de ir en cada rectángulo, avisa a tu docente.
- El docente te mostrará las respuestas correctas. Pega la gráfica en el recuadro correspondiente.
- Revisa esta otra hoja de trabajo similar a la tuya. ¿Qué comportamientos ves en las gráficas? ¿El resultado es similar al que obtuviste tu?
Otra hoja de trabajo (haz clic hasta que llegues a esta parte de la actividad)
¿Ves algún patrón en las gráficas? Discutelo con tu docente y compañeros.
¿Qué nos dice el Teorema del Límite Central?
Sean \(X_1\), \(X_2\), …, \(X_n\) variables aleatorias independientes e idénticamente distribuidas con media \(\mu\) y varianza \(\sigma^2<\infty\). Entonces, para cualquier \(x\in\mathbb{R}\)
\(\lim_{n\rightarrow\infty}P[\frac{\bar{X}_n-\mu}{\sigma/\sqrt{n}}\leq x] = P[Z\leq x]\) donde \(Z\sim N(0,1)\).
Esto es equivalente a que, para \(n\) suficientemente grande \(\bar{X}_n\sim N(\mu, \frac{\sigma^2}{n})\).
Discusión final
- ¿Cuál es la diferencia entre la Ley de los Grandes Números y el Teorema de Límite Central?
- ¿Están conectados estos dos teoremas o tiene una relación?
- ¿Cuál es la relación entre la distribución de la población y la distribución muestral de la media?
- ¿Cómo podemos describir la distribución muestral de las medias sin realizar simulaciones?
- Para muestras aleatorias de tamaño 100 de una población de temperaturas corporales humanas, ¿cuál sería la forma, el centro y la dispersión de la distribución de las medias muestrales? Recuerda que la distribución de temperaturas en humanos es normal con media \(\mu=\) 36.7°C y con una desviación estándar de \(\sigma=\) 0.6°C.
- ¿Y cuál sería más probable que se acercara más a 36.7 ° C: una temperatura media basada en 9 personas o una temperatura media basada en 25 personas?